Tech Talks: Comparison between Linear and Binary Search Algorithm

Linear Search Algorithm

• An algorithm to find if a certain element exists in a given array or not.
• Linearly iterate the array to find the required element.

It has a time complexity of Big-O(N) which gives us a linear graph.

Binary Search Algorithm

• An algorithm to find if a certain element exists in a given array or not.
• The array must be sorted.
• Find the middle element of the array and then compare it with the target element.
• Let’s say the array is sorted in ascending order, if the middle element is smaller than the target element we only have to check for the array after the middle element and this saves time.

We can perform the same algorithm on the shortened array until we find the target element.

After shortening the array if at some point the start element is greater than the target element then the element does not exist in the array.

It has a time complexity of Big-O(log(N)).

Here is an example :

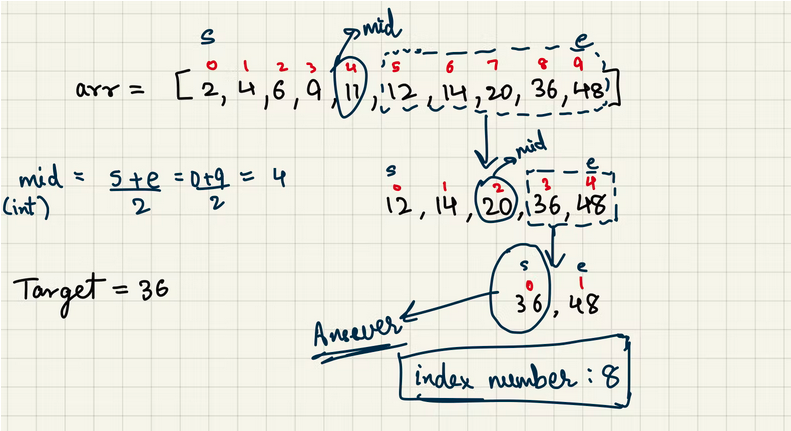
After learning about each algorithm we can clearly see that Binary Search is a better algorithm but let’s find out by how much it leads! (you might be surprised)

In a hypothetical situation say we have to find an element in an array containing 1000000 elements For now, let’s take the worst case: our target element does not exist in the array.

For Linear Search Algorithm we would have to iterate through the complete array which would cost us 1000000 iterations!

For Binary Search Algorithm we would have to search for the element by comparing it with the middle element of the array which would take us log(1000000)/log(2) iterations to search in the array. If you calculate this, you would end with just 19.93 iterations (roughly 20 iterations)!

So if we compare both of them, Binary Search is 50000 times faster than Linear Search Algorithm which clearly makes it a preferable algorithm.